Beberapa waktu lalu sudah ada 3 metode yang saya tampilkan pada kategori Metnum.
Selanjutnya adalah metode Aitken. Metode ini merupakan Kelanjutan dari metode Iterasi, namun sedikit berbeda pada algoritma ke 3 nya.
Pada metode aitken terdapat perhitungan selisih dari nilai X awal dan X berikutnya.
Kelebihannya sudah jelas tentu lebih cepat dibandingkan dengan metode iterasi namun pada kelemahannya adalah Error yang cukup besar.
Pengulangan dari metode iterasi hanya sampai batas n=3. jadi kita dapat menggunakan logika struktur kontrol pengulangan FOR, DO WHILE dan REPEAT UNTIL.
Namun saya sendiri (Author Blog) belum berhasil membuat Kodingan yang benar-benar sempurna. Dalam kata lain masih ada sedikit Pemicu agar Output program sesuai dengan Keinginan.
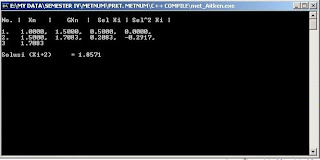
Berikut Tampilan Tabelnya :
contoh soal Xawal = 1 dan Error = 0.01
Selanjutnya adalah metode Aitken. Metode ini merupakan Kelanjutan dari metode Iterasi, namun sedikit berbeda pada algoritma ke 3 nya.
Pada metode aitken terdapat perhitungan selisih dari nilai X awal dan X berikutnya.
Kelebihannya sudah jelas tentu lebih cepat dibandingkan dengan metode iterasi namun pada kelemahannya adalah Error yang cukup besar.
Pengulangan dari metode iterasi hanya sampai batas n=3. jadi kita dapat menggunakan logika struktur kontrol pengulangan FOR, DO WHILE dan REPEAT UNTIL.
Namun saya sendiri (Author Blog) belum berhasil membuat Kodingan yang benar-benar sempurna. Dalam kata lain masih ada sedikit Pemicu agar Output program sesuai dengan Keinginan.
Berikut Tampilan Tabelnya :
contoh soal Xawal = 1 dan Error = 0.01
Metode Aitken:
Kodingan :
#include<iostream.h>
#include<conio.h>
#include<stdio.h>
#include<math.h>
void main()
{
float X,GX,GXn,E,A,SelXi,del,x,temp; //deklarasi variable
E=0.01;
int n=1;
printf("\nNo. | Xn | GXn | Sel Xi | Sel^2 Xi |\n\n");
X=1;
for (n=1; n<=2; n++)
{
GXn=(pow(X,2)+8)/6; //X n+1 = G (Xn)
SelXi=GXn-X;
del=SelXi-0.5;
printf("%d. %1.4f, %1.4f, %1.4f, %1.4f,\n",n,X,GXn,SelXi,del);
X=GXn;
}
printf("%d %1.4f",n,X);
cout<<" "<<X;
cout<<" "<<del;
x=X - (pow(SelXi,2)/del);
printf("\n\nSolusi (Xi+2) = %1.4f",x);
while(n==1){
cout<<"\nnih "<<SelXi;
n--;
}
getch();
}
INGIN MERASAKAN KEMENANGAN DI DALAM BERMAIN TOGEL TLP KI ANGEN JALLO DI NMR (_0_8_5_2_8_3_7_9_0_ 4_4_4_) JIKA INGIN MENGUBAH NASIB KAMI SUDAH 20 X TERBUKTI TRIM’S ROO,MX SOBAT
BalasHapusINGIN MERASAKAN KEMENANGAN DI DALAM BERMAIN TOGEL TLP KI ANGEN JALLO DI NMR (_0_8_5_2_8_3_7_9_0_ 4_4_4_) JIKA INGIN MENGUBAH NASIB KAMI SUDAH 20 X TERBUKTI TRIM’S ROO,MX SOBAT